The quality of a part punched by the sheet metal forming process is directly related to the tribology and the frictional conditions acting in the process. The friction conditions depend on sheet material, tool material, lubricant, surface roughness, normal forces, deformation speed and other factors. This combination of factors is called a tribological system. Tribology is defined as the science and technology of interaction between surfaces with relative motion among themselves and the phenomena that recur according to Jost, 1966 [1], who also reported that it is something that is present at practically all interfaces where motion occurs, including the contact of air against the surface of a moving car.
Recent studies indicate that the costs associated with friction represent about 5% of the final production value of the part [2]. In 1966 Jost [1] reported that tribology comprises several areas, such as chemistry, physics, solid mechanics, heat transfer, materials science among others. The literature also points out that the study of tribology is essential for both economic and environmental reasons, and it is mentioned that about 10% of the world’s crude oil consumption is used to overcome friction. Holmberg et al., 2017 [3] conducted. a study to assess the impact of tribology on global energy consumption, costs and emissions. The study covered the transport, industrial, residential and service sectors. They found that 23% of global energy consumption is due to tribological contacts, where 20% is used to overcome friction and 3% to produce new components to replace worn ones. They also report that with new technologies in surface treatments, materials and lubricants, it will be possible to reduce energy consumption with friction-related losses by 40% over 15 years and by 18% over 8 years.
The first numerical friction models were investigated in the 1980s, when Bin and Luo, 1988 [4] applied the finite element method in their study to predict stress distribution and apparent friction, proving also the existence of phenomena by experiments. Hol et al., 2015 [5] presented a friction model for large-scale use in conformational simulations based on micrometric surface changes. Currently, software programs are proposing a new technology to simulate the tribological conditions in a forming process by assigning parameters to the tools, sheet material and lubricant to create more realistic surfaces. From the relative motion and interaction between these surfaces, the roughnesses are deformed and the coefficients of friction are determined for use in forming simulation software.
In the context presented, the aim of this paper is to present for discussion some works developed in the Bruning Tecnometal R&D department with the purpose to fill a gap related to friction in the simulation, resulting in more realistic and thus more complex tribological models.
DESCRIPTION OF THE TRIBOLOGICAL SYSTEM
In this study, the material of the tool used to simulate the tribological system was hardened and tempered AISI D2 steel with a hardness of about 59±1 HRC, having a composition according to Table 1. The tool was polished by hand and treated with a CrAlN coating, which is widely used in forming tools. The sheet metal used in the numerical simulation was a cold rolled and hot-dip galvanized steel of class CR4 with an initial diameter of 160 mm and a thickness of 0.65 mm, having a final geometry as illustrated in Figure 1.
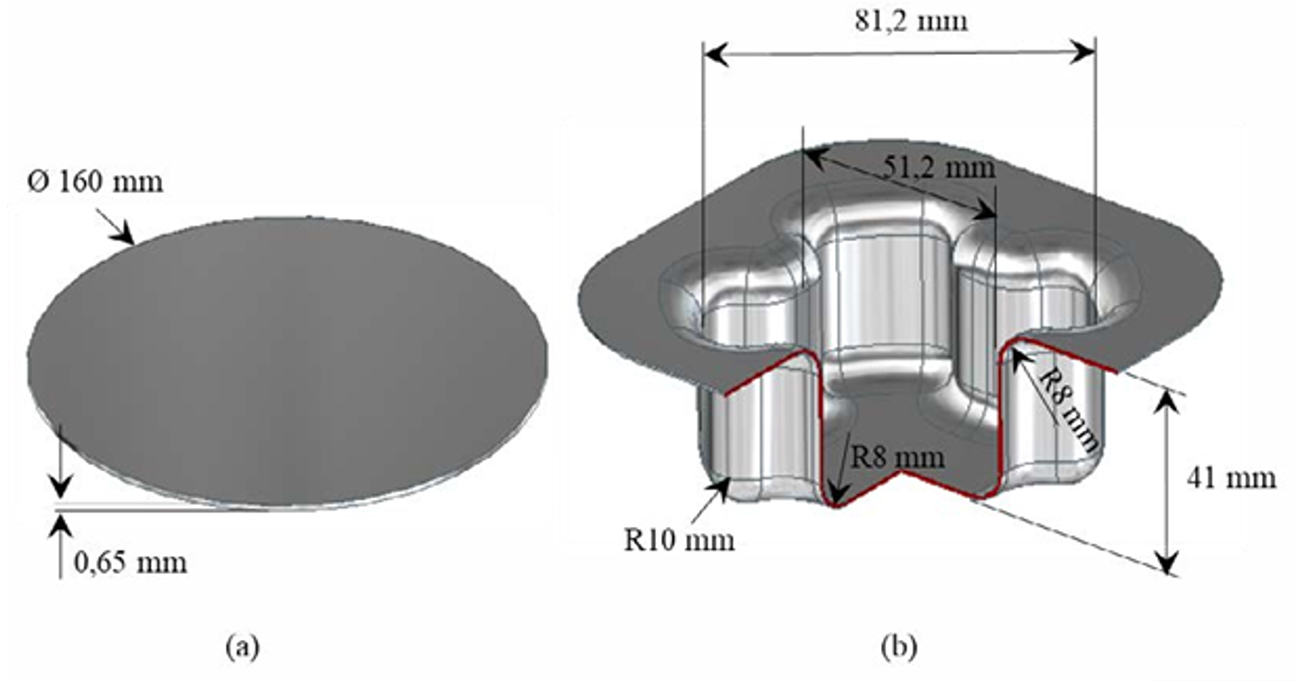
Figure 1: Dimensions and geometry of the sheet (a) and of the finished part (b).

Table 1: Chemical composition of the tool steel AISI D2.
For the mechanical characterization of this material, test specimen No. 5 taken from the standard JIS Z 2201:1998 was used. In Table 2 are shown the results obtained from the tensile test in the three directions in relation to the rolling direction of the sheet: 0°, 45° and 90°.
By applying the standards DIN EN ISO10113 and ASTM E-517, the indexes of plastic anisotropy and the work har-dening exponent were determined, the results are shown in table 3.
As well as the mechanical properties, it was necessary to characterize the sheet metal/tool surfaces, which should be used as input data for the simulation of the tribological system. For this purpose, earlier studies developed at Bruning Tecnometal found mean tool roughness values of 1.3 µm with a standard deviation of 0.04 µm and a sheet roughness of 1.6 µm with a standard deviation of 0.09 µm [6]. Karapannasamy et al., 2014 [7] used a surface roughness of 0.08 µm for a stoned tool and Hol et al., 2016 [8] achieved a roughness of 1.35 µm for a hot-dip galvanized sheet in their experiments. Therefore, three tool roughness profiles were evaluated using the TriboForm® software.
Hol et al., 2016 [8] used quantities of 0.5 g/m² and 1.2 g/m² in a friction test of the strip drawing type, while Sigvant et al., 2018 [9] used 2 g/m² in a case study with stamped automotive components, thereby performing a numerical and experimental assessment. Hol et al., 2017 [10] used quantities of 0.6 g/m² and 2 g/m² on each side of the sheet and analyzed the influence of the lubricant quantity on the final quality of the product.
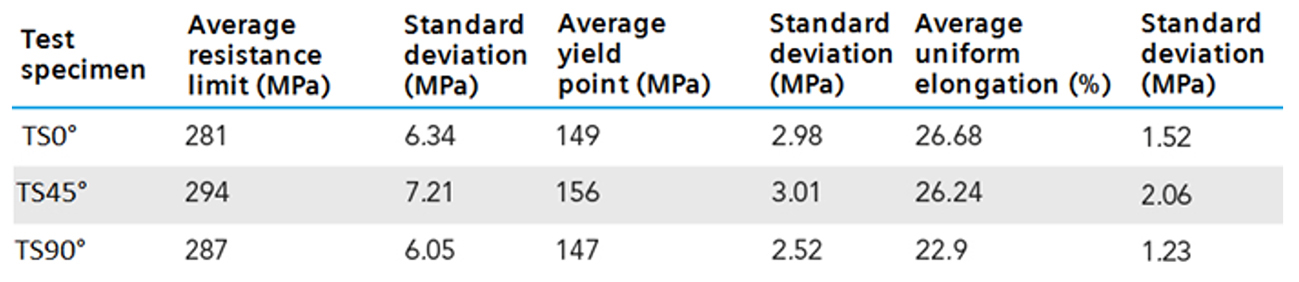
Table 2: Mechanical properties of the material.
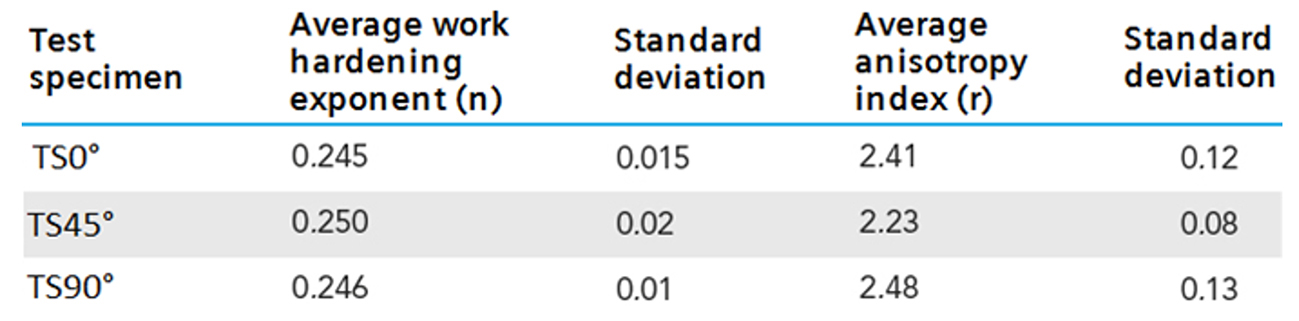
Table 3: Coefficients “n” and “r” for each rolling direction.

Figure 2: Topography of the tool surface with roughness of (a) 0.08 μm, (b) 0.4 μm (b) and (c) 1.3 μm.
In this study, in order to eliminate surplus variables, the quantity of lubricant fixed of 1.2 g/m² was considered.
PLANNING OF THE EXPERIMENT
The study considers a fixed amount of lubricant of 1.2 g/m², fixed sheet surface roughness of 1.6 µm for all case studies and evaluates the influence of different tool surface roughness, which are 0.08 µm, 0.4 µm and 1.3 µm, as described in detail in Table 4. In addition to the three conditions examined, the Coulomb coefficient constant of 0,15 was also applied for comparison purposes.
The numerical analyses employed in this case study were carried out using TriboForm® software in combination with Autoform®. Lastly, the methodology and simulated tribological system followed the flow chart in Figure 3.
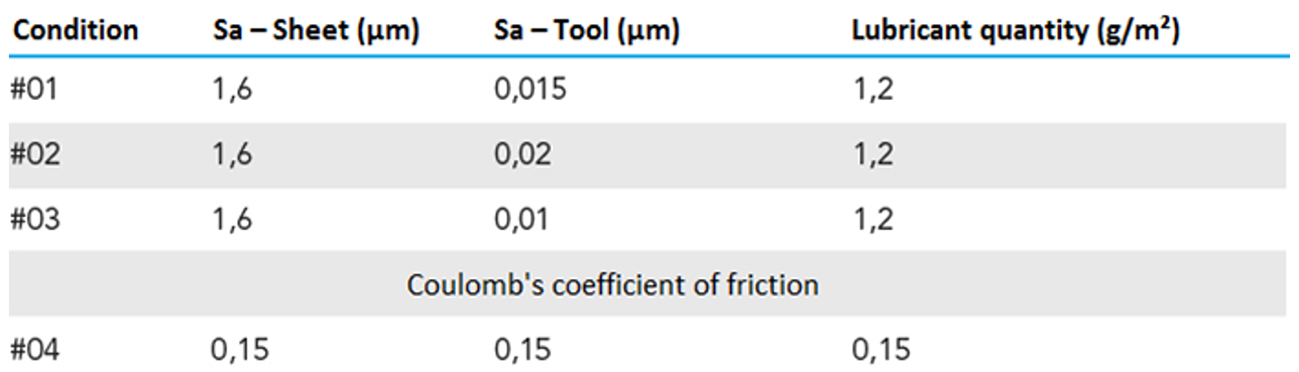
Table 4: Planning of the simulated tribological system.
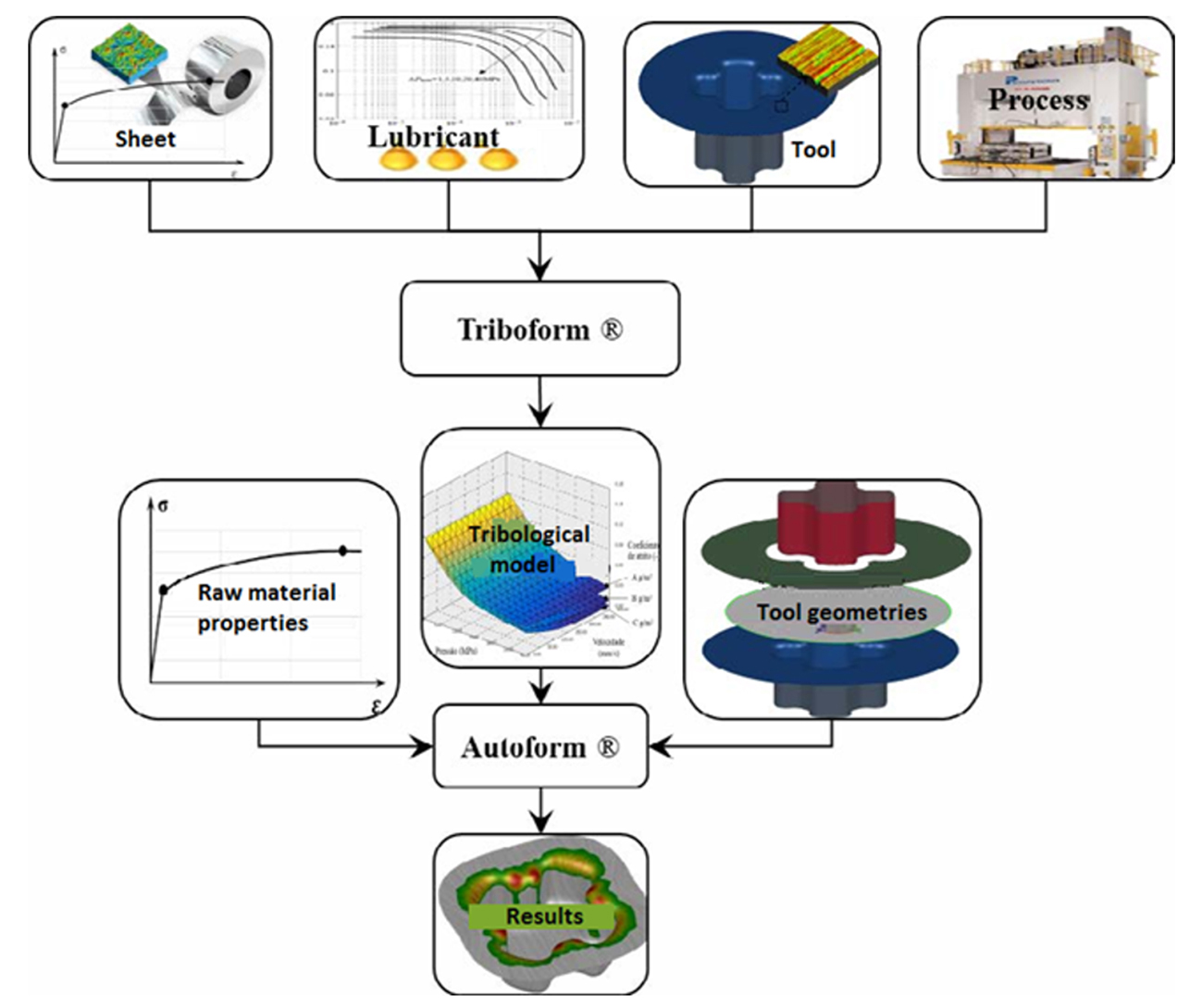
Figure 3: Study methodology.
RESULTS AND DISCUSSION
The simulation results evaluated in this study were the coefficient of friction and tool roughness, as well as the influence of the interaction of both on the tribological system. Figure 4 comprises the tribological models from case studies #01, #02 and #03, where the amount of lubricant is 1.2 g/m² and the sheet roughness is 1.6 µm. All three models are differentiated by the tool roughness used in each case.
On the whole, it is clearly observed that tool roughness has a very high impact on the generated tribological models. While for the roughness of 1.3 µm on the tool holds maximum coefficient values of 0.25, the stoned tool with a roughness of 0.08 µm shows maximum coefficients of 0.05.
The results obtained in the simulation were compiled and are shown in Table 5.
From the results of Table 5 it can be concluded that the higher the roughness of the tool/sheet, the higher the variation of the coefficient of friction during forming, and the second most impacting factor will be the contact pressure. The higher the contact pressure, the lower the friction presented. Figure 5 verifies such relationship, where the regions with the highest pressures are located in the entrance radii of the die face and on the punch radii.

Figure 4: Tribological models with different tool roughness and projectionof Coulomb’s coefficient of friction with deformations equal to 0 (a) and 0.4 (b).

Table 5: Simulation results of the investigated tribological conditions.
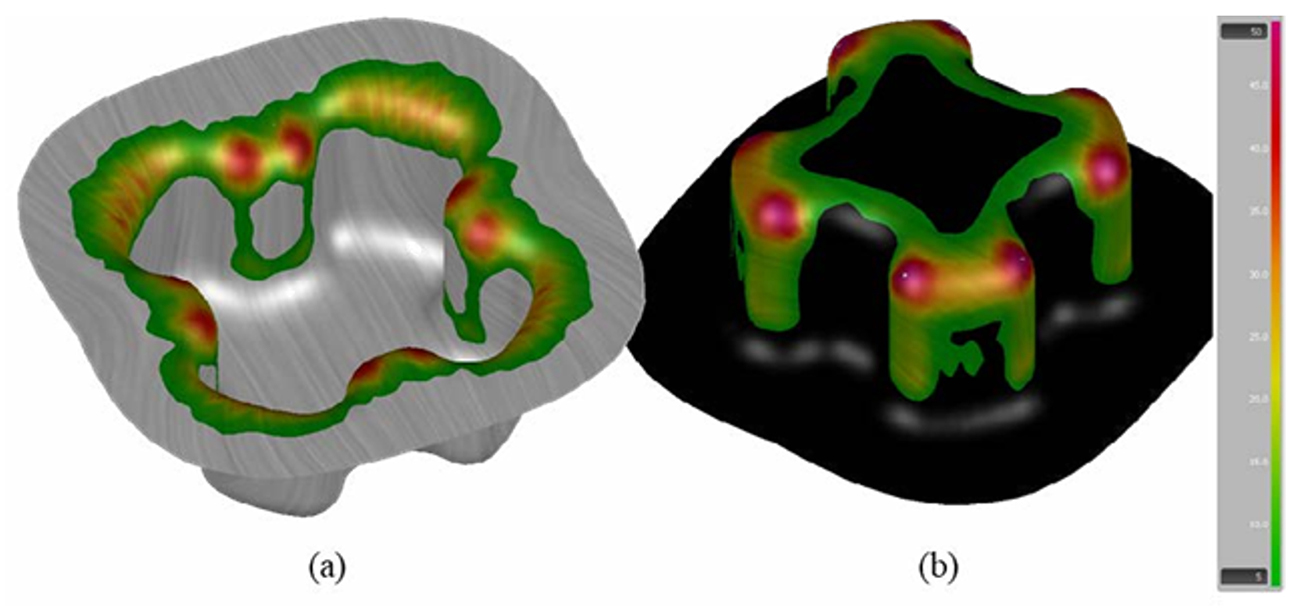
Figure 5: Contact pressure distribution in MPa in the die face (a) and punch (b).
Regarding the coefficient of friction obtained in the simulated models, we observe the results of cases #01 (a), #02 (b) and #03 (c) in Figure 6, where the coefficient of friction in the radius quadrant presented results in the range of 0.03 in the three parts, but there was a significant increase in the flange and lateral wall regions. On the whole, the coefficients of friction obtained in the evaluated regions increase according to the higher tool surface roughness.
According to the graphs in Figure 7, we can observe that the resultant force of the punch increases with rougher surfaces, particularly when compared to the constant Coulomb friction of 0.15, and that the higher the roughness, the higher the thinning and the smaller the final thickness
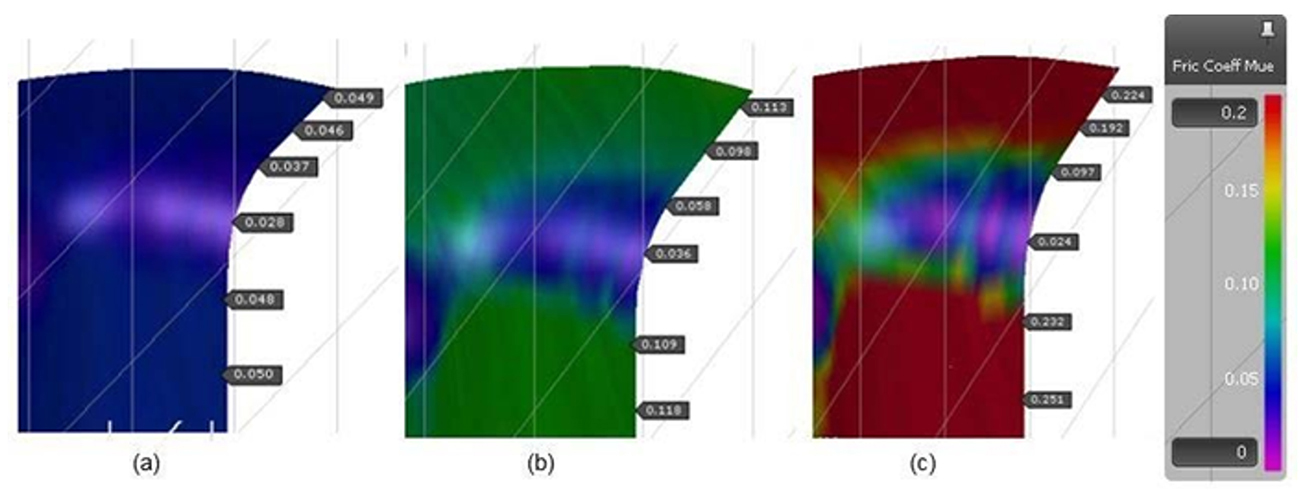
Figure 6: Friction coefficient distribution at the die face radius for case studies (a) #01, (b) #02 and (c) #03.
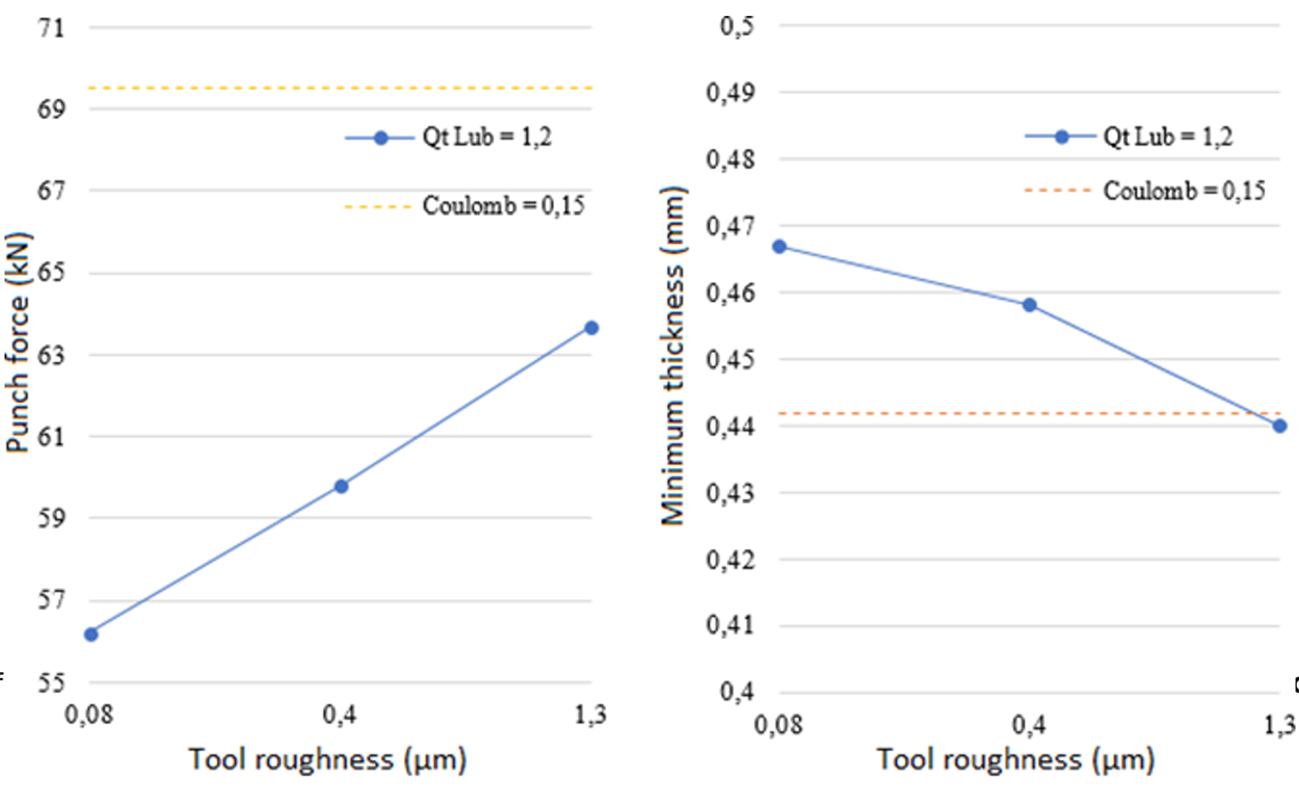
Figure 7: Graph of (a) maximum punch force and (b) minimum thickness in accordance with the tool roughness under the three conditions evaluated in comparison with the Coulomb friction.
CONCLUSIONS
On the basis of the present work it can be concluded that under the three roughness conditions investigated for the simulation of the forming process, the tool surface roughness of 0,08 µm was the one that resulted in a lower forming force. Regions with higher contact pressures were located in the bending radius of the die face and resulted in the lowest friction coefficient values. Furthermore, it is observed for all investigated cases that there is a difference in the force results between the Coulomb model and the tribological models.
Because the surface roughness has a significant impact on the results, it can be an obstacle to obtaining accurate results in the large-scale production chain, as the surface preparation process usually does not guarantee uniformity across the entire area, particularly on very large areas. An alternative to bypass this problem is the identification of the most critical and sensitive regions in the simulation and prioritization of finishing in these regions.
ACKNOWLEDGMENTS
The authors are very grateful to the partners TriboForm and AutoForm for their long-standing partnership and for the collaboration and knowledge needed to conduct this work.
Ibson Ivan Härter – Mechanical Engineer graduated at UNIJUI, Brazil, Master’ Degree in Mechanical Engineering at the Universidade Federal do Rio Grande do Sul (UFRGS/PROMEC), Brazil. Responsible for simulations of stamped parts, where he works as Tool Simulation Specialist at Bruning Tecnometal Ltda., Panambi/RS, Brazil.. ibson@bruning. com.br
Rogério José Marczak – Mechanical Engineer and Master’ Degree in Mechanical Engineering graduated at the Universidade Federal de Santa Catarina, Brazil, PhD in Civil Engineering graduated at the Universidade Federal do Rio Grande do Sul, Brazil. He is currently full professor in the Department of Mechanical Engineering and a member of the GMAp – Applied Mechanics Group of the UFRGS, and is dedicated to the research and development of numerical methods for linear and non-linear continuous media problems, as well as vehicle simulation and analysis techniques. rato@mecanica.ufrgs.br
Diego Tolotti de Almeida – Mechanical Engineer graduated at UNIJUI, Master of Science and Material Technology with emphasis on friction welding processes. Doctoral Student in the Graduate Program in Mining, Metallurgy and Material Engineering (PPGE3M). Laboratory of Metal Physics (LAMEF/UFRGS). Research and Development Officer at Bruning Tecnometal Ltda. in Panambi/RS, Brazil. diegot@bruning.com.br
Angélica Paola de Oliveira Lopes – Production Engineer graduated at UNICRUZ – Universidade de Cruz Alta, Brazil. Research and Development Technician at Bruning Tecnometal Ltda. in Panambi/RS, Brazil. angelica@bruning.com.br
Daniela Bertol – Materials Engineer and Master of Science and Material Technology by the Post-graduate Program in Mining, Metallurgical and Materials Engineering (PPGE3M), UFRGS. Research and Development Senior Analyst at Bruning Tecnometal Ltda. in Panambi/RS, Brazil. daniela.bertol@bruning.com.br