Can You Decrease Blank Sizes to Save Money Without Consequences?

Introduction

In the sheet metal forming industry, it is a common practice to decrease blank sizes as much as possible, with the goal of saving material and therefore money.

This step is usually performed at the end of the tool tryout phase or at the beginning of part production, if it hasn’t already been completed during the engineering phase.

It’s immediately apparent that this optimization allows companies to save millions per year, but can we say with certainty that this is always the case? Are there any resulting consequences for the part production that result from such minimization that have been overlooked?

Surely there will be ramifications of some sort, but the question is: are they acceptable? In other words, are we certain we are actually saving money overall?

It’s important to examine the real knock-on effects.

This is exactly the evaluation that the engineering department of an automotive part maker wanted to perform: a deep analysis of the consequences of reducing the blank size on the stability of the production.

So with this end in mind, where should we begin the investigation? What parameters will we need to include and what result variables should we check to determine the blank optimization effectiveness?

We have already mentioned that the blank optimization is done in tool tryout, where the material of the blank has precise characteristics (thickness, yield stress, etc.). The question to ask ourselves is: does this scenario 100% reflect the production scenario? And the answer is no. Material for production, even possessing characteristics within a certain range, will likely be different because they come from another coil (check the value’s distribution of the different characteristics) with differing amounts of lubrication, strokes per minute, press type, and blank position.

In order to account for these differences, robustness checks on different blank sizes are required to simulate the expected outcome of a part production process in advance. This will ensure the results are suitable when considering process parameter variation. In other words, robustness checks account for the noise of variables that cannot be controlled during production. In our example we consider:

• Lubrication
• Binder force
• Sheet thickness
• Average material r-value (material anisotropy)
• Material yield stress and tensile strength (interdependent through a correlation factor)

Example: Door Inner

As an example, we can consider the complete process including springback of manufacturing a door inner (two parts in one tool). The evaluation criteria involves checking the following parameters:

1. Price: The lowest possible price of the nested blank
2. Draw-in: After D-30 drawing operation, the blank edge should not pass the inner drawbead (minimum 4mm distance from the center line of the bead – yellow line in Figure 1)
3. Defect rate for splits: Estimate defect rate related to splits during production at the end of D-30 by checking the max failure result with max value set to 1; current nominal result fulfils the requirements being equal to 0.946 at maximum
4. Springback stability: ±0.5mm springback tolerances of the final part

Of course, additional quality criteria could be taken into account, but we will keep the concept as simple as possible for this blog article. For the blank modification itself, the draw-in of the nominal blank on all three sides (we consider symmetry) is already very close to the inner drawbeads (see Figure 1). The width of the blank (1300mm) must be constant, as a modification would violate criteria #2 of the above list. Nevertheless, the two corners above and below offer potential to minimize the blank size in the x-direction, as shown in Figure 1. So in our simulation, both points will be defined as interdependent design variables (i.e., can be controlled) in the x-direction with a variation range of ±30mm for the robustness setup. This allows the users to evaluate the robustness of different blank sizes simultaneously in one AutoForm-Sigma analysis.

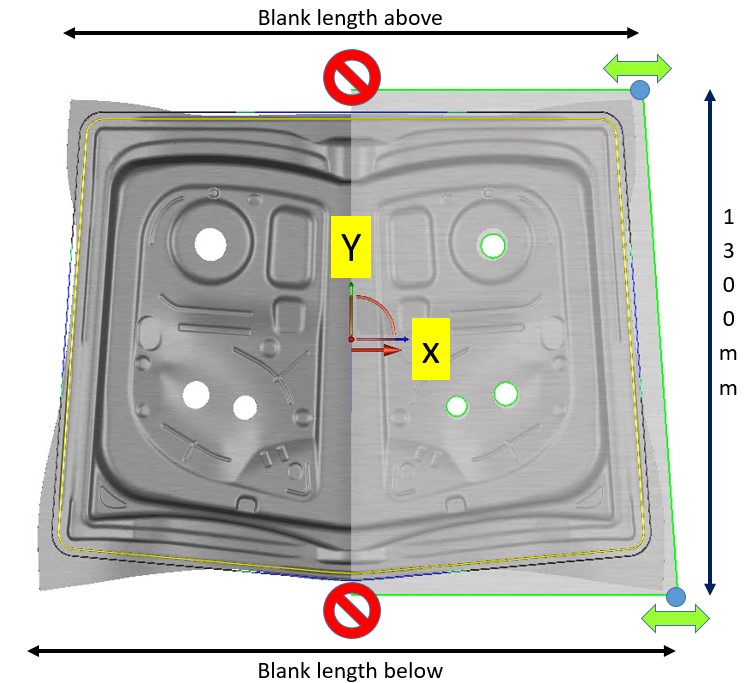
Figure 1: Green curve = nominal blank; formed sheet = draw-in of the nominal blank; yellow curve = inner drawbead

Now we’ll take a look at the results.

Results

Before deciding on the optimum blank size, we first examine the robustness of the engineering intent.

Nominal blank

• Blank size: 1500mm length above & 1680mm length below.

The result of the robustness analysis with the nominal blank leads to the following output:

1. Price: 9.27€ (Figure 2)
2. Draw-in at end of D-30: fulfilled (Figure 1)
3. Defect rate for splits at the end of D-30: > 10.7% (variation of max failure based on production parameter variation: 0.727 – 1.2). Note: The single simulation with nominal blank fulfilled this limit; nevertheless, the robustness check shows that there is a sensitive area for noise variables that leads to this defect rate (Figure 3). This means that in tool tryout or production, we can experience splits if the material or the other noise parameters differ from what was used in the single simulation (the engineering intent).
4. Springback stability of the final part: very stable springback behavior except for a small local orange area (unreliable) with a defect rate of > 0.007% (Figure 4)

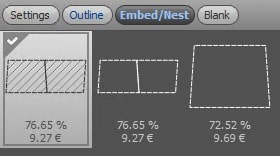
Figure 2: Lowest price based on optimal nested blanks for the nominal blank

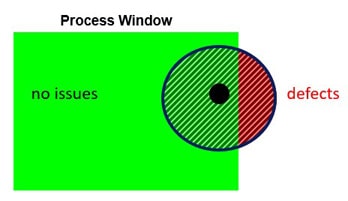
Figure 3: Single simulation result vs. robustness check result – the importance of process window detection

Figure 4: Springback stability (CP-value) for the nominal blank

Optimized blank

Once the calculation of the possible input-output combinations was over, we were able to compare the results and look for the smaller blank size that ensured compliance with the constraints previously listed:

• New blank size: 1525mm length above & 1633mm length below.

The results of the robustness analysis generated by the optimized blank are as follows:

1. Price: 9.21€ (figure 5) à savings of 0.06€ per blank compared to nominal blank
2. Draw-in limitations at end of D-30: fulfilled
3. Defect rate for splits at the end of D-30: > 3.1% (variation of max failure during production parameter variation: 0.66 – 1.118)
4. Springback stability of the final part: still very stable springback behavior, except a small local orange area (unreliable) with a defect rate of > 0.3% (Figure 6)

Figure 5: Lowest price based on optimal nested blanks for the optimized blank

Figure 6: Springback stability (CP-value) for the optimized blank (=blue curve; nominal blank = green curve)

Conclusions

As shown in Table 1, it is indeed possible to decrease blank size to save money without negatively impacting production (same stability). The optimized blank would actually lead to a much lower defect rate of splits (lower reject rate in production à additional saving) by achieving comparably stable springback behavior. In addition, we save six Euro-cents per blank compared to the initial engineering intent blank size! So, is it worth taking this approach in the end? It is, without a doubt in this case.

Table 1: Summary of the results for both blanks and criteria

To more accurately estimate the total savings, we must refer to the part cost on a certain production volume. Assuming a production volume of 2 million (car life cycle), as shown in Figure 7, we save 0.49€ per part. Over the entire life cycle, this translates to a savings of 980,000€ – not a bad return on investment for a few hours of simulation during the engineering phase!

For completeness, we should also mention that a more stable process reduces the number of interruptions during production to adjust process parameters as the production evolves. We will further discuss this aspect in a subsequent blog, as die line downtimes represent a very relevant production cost.

Figure 7: Total cost per piece – normal blank versus improved blank

Now we should ask the question: can we always expect that decreasing the blank size to save money will not have negative consequences for any part of the process? Of course not! We have to comprehensively evaluate every project individually. However, this kind of analysis will help designers to make the most beneficial decisions and potentially avoid negative surprises in tool tryout or production.