Sheet metal forming is a cornerstone of mass production, producing complex shapes with high accuracy and minimal waste. This intricate process involves several stages and parameters, including material properties, tool geometry, lubrication, and process parameters. Evaluating these factors requires accurate deep drawing simulations. It is widely agreed that tribological phenomena between the workpiece and the tool significantly influence accuracy.
For the current study, Mondragon University and Ford analyzed a complex numerical model and compared it with experimental measurements. This included a mechanical characterization of the material and analysis of the topography, along with several strip drawing tests. The study examined the variability in mechanical properties and friction across five batches of the same material from the current supplier. From these tests, different tribological models were developed to enhance simulation models.
The material in focus was DC06 cold-rolled mild steel, 0.65 mm thick, with a hot dip galvanized (50G50G-GI) coating. The steel maker applied Electro Discharge Texturing (EDT) to the sheet material, aiming to improve the tribological system. Tensile tests were performed along each rolling direction, and Nakajima tests determined the Forming Limit Curve (FLC). Additional tests were carried out to obtain suitable yield criteria.
To analyze the surface topography, the primary surface parameters of the sheet material were computed using metrology software. The characteristic features of the surfaces were evaluated using a set of topographical parameters. Recording and measuring press and process parameters are critical for developing an accurate numerical model. Thus, tool roughness and lubricant distribution in different zones of the part were measured in Ford’s workshop.
The tribological conditions were characterized using strip drawing tests. The test machine, developed by Mondragon University, consists of two closed-loop-controlled servo-driven axes that apply normal force and tangential movement. To gauge their impact on the numerical results, three models were evaluated: a constant friction coefficient, a pressure and velocity dependent coefficient (P-v dependent), and the TriboForm friction model with varying lubrication zones.
The case study involved a mild steel inner car door panel, produced by Ford Valencia in Spain. This industrial component features complex geometries, stretched curvatures, and harsh transitions.
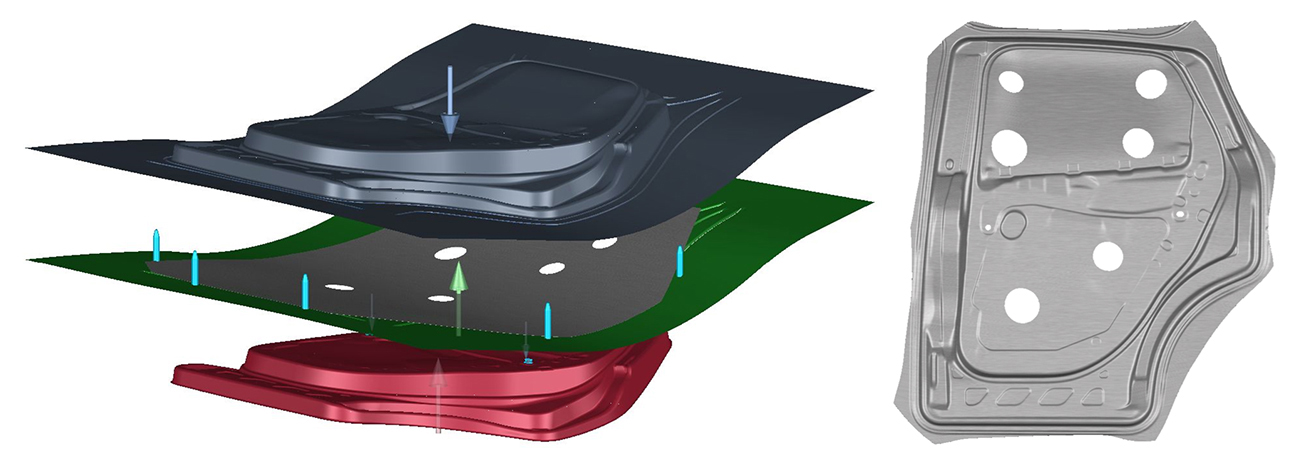
Figure 1. AutoForm model set-up (left) and final part (right).
Figure 2 illustrates the Forming Limit Diagrams (FLDs) of the car inner door panel using the three tribological models. As the complexity of the friction model increases, a decrease in the overall stretching state of the component is evident. Using the traditional constant friction model employed in industrial simulations resulted in severe splits in several zones of the part. Conversely, the P-v-dependent and TriboForm models reported a drastic change in the FLD, delivering a valid process with no splitting risks.
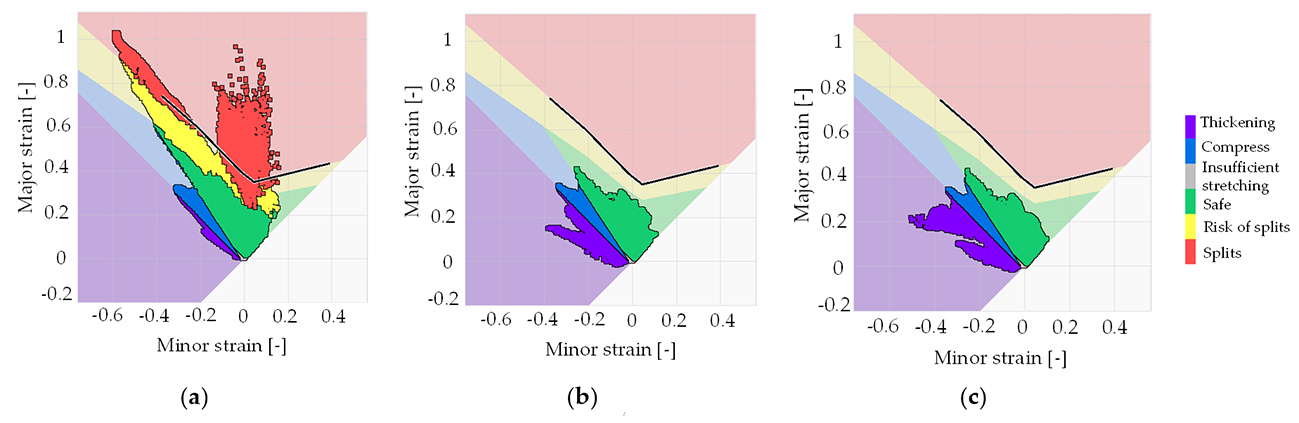
Figure 2. Simulation results of FLDs for the part using the three tribological models: (a) constant (µ=0.15); (b) P-v dependent; and (c) TriboForm with lubrication zones.
To analyze the draw-in measurements, 11 points were selected based on production data, with their coordinates remaining consistent across all three numerical models (as shown in Figure 3). This figure compares the draw-in differences of the P-v-dependent and TriboForm models, in relation to the constant model.
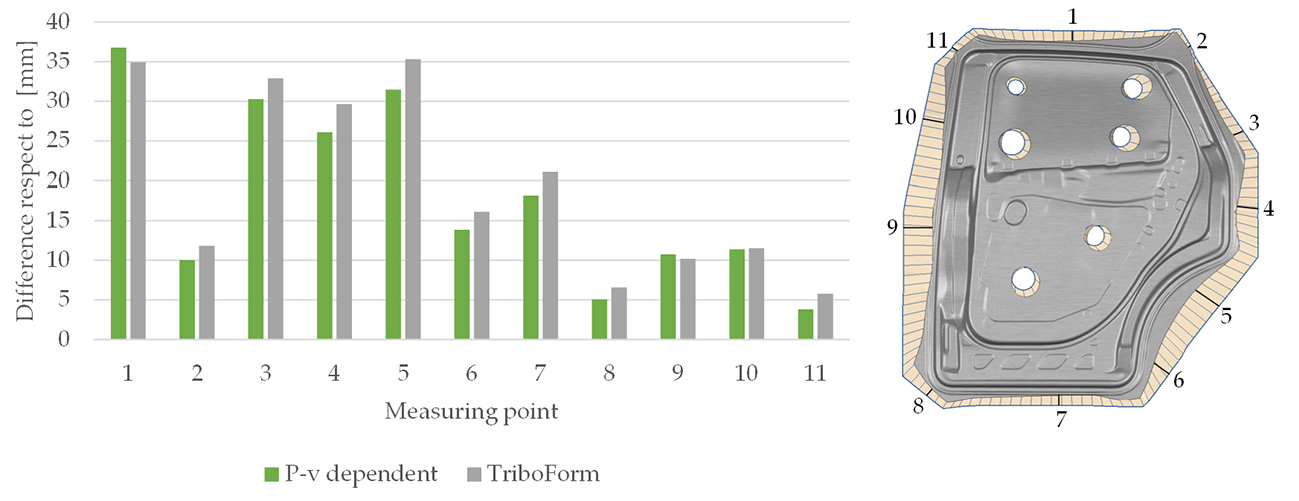
Figure 3. Difference in draw-in prediction for P-v-dependent and TriboForm models vs. the constant model at the eleven selected points.
In the industrial process, the FLD of three critical zones of the part was selected for a numerical–experimental comparison. Figure 4 illustrates the experimental FLD contours for one of the selected zones, while Figure 5 shows the differences between the numerical draw-in and experimental measurements.
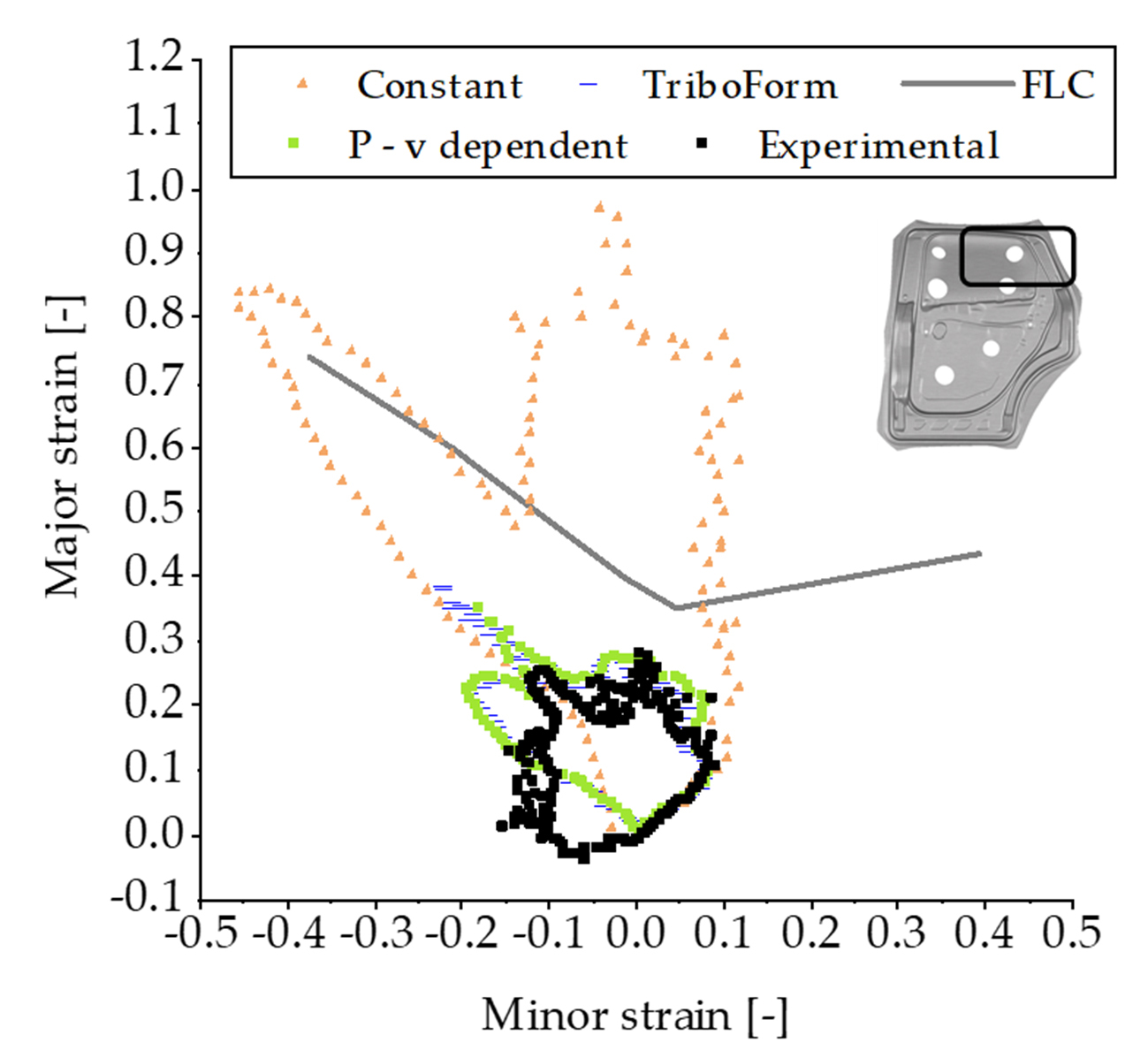
Figure 4. FLD contour diagram of a selected zone in the industrial part: tribological models (constant, P-v dependent, and TriboForm) vs. experimental data
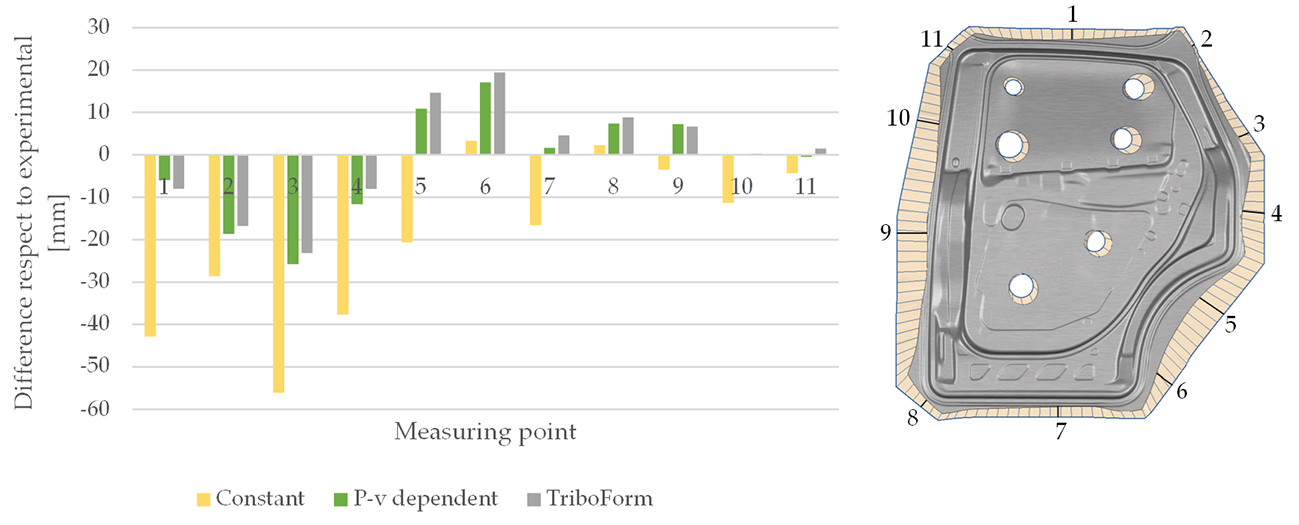
Figure 5. Comparison of numerical draw-in using the three tribological models against experimental values for the 11 points analyzed.
The use of complex tribological models, where the friction coefficient is a function of contact pressure, sliding velocity, and lubricant quantity, improved the simulation accuracy compared with the constant model. The TriboForm model with lubrication zones and the P-v-dependent models yielded similar results, with TriboForm predicting slightly more thickening. Across all measured points, the constant model predicted a lower draw-in value than its more complex counterparts. Comparing these findings with the experimental results revealed no clear trend. Furthermore, no significative differences in the friction coefficient were observed across the different material batches. This suggests that a variation in sheet roughness, an uncontrollable factor that is not batch dependent, did not significantly affect the friction coefficient results. Further research will analyze the influence of tool stiffness on the tribological behavior, FLD, and draw-in results.
Readers can access the original study here: On the Use of Advanced Friction Models for the Simulation of an Industrial Stamping Process including the Analysis of Material and Lubricant Fluctuations (https://www.mdpi.com/2075-4442/11/5/193). This research was led by Dr. Lander Galdos and Laura Muñiz from Mondragon Unibertsitatea.