As already discussed in the post “Constitutive modeling of sheet metal” there are four main components needed to model the plastic deformation of sheet metals: yield function, hardening model, flow rule, and failure model. These concepts have theoretical backgrounds based on continuum mechanics of materials. However, since they represent physical material behavior, all of these concepts can be visualized through diagrams, which can be very useful for understanding and comparing material behavior. A few of these concepts will be discussed below.
Follow these links to see part one, three and four.
Yield function
Yield functions are used to determine if a given 3-D stress state is large enough to initiate or prolong permanent deformation, or plastic flow. For that purpose, multidirectional components of the shear stresses and normal stresses are used to compute a scalar value or equivalent stress (effective stress). Afterward, this equivalent stress is compared with the current yield stress of the material to determine if the material is flowing plastically or not. For that reason, these expressions are also called yield surface, yield conditions, or yield criteria.
The first studies regarding yield conditions go back to Tresca (1864) and von Mises (1913). Isotropic yield functions, such as Tresca and von Mises, consider the material as a perfectly homogeneous continuum. In reality, sheet metals possess a microstructure as a result of the rolling operations in the production stage. This microstructure generates a directional dependency of the plastic properties, which is called anisotropy. Isotropic yield functions cannot reflect this directional behavior. For that reason, anisotropic yield functions are often utilized, such as Hill, Barlat or BBC. In anisotropic yield functions, sheet metals are assumed to be orthotropic, whereby the rolling direction (RD or 0°), the transverse direction (TD or 45°), and the normal direction (ND) form the symmetry axes.
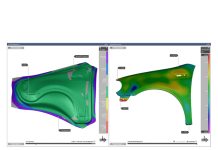
Yield functions are visualized generally with the help of a diagram plotted in stress space. This plot is called a yield locus or yield surface. Yield criteria developed for sheet metal forming are functions of three stress components: two normal stresses and one shear stress component. Therefore, they could be plotted in 3-D stress space with the axes σx, σy, and τxy. The shape of these plots is usually an ellipsoid.

However, a 3-D graphical presentation method is difficult to work with. Therefore, in most simulation tools, textbooks, or research papers, these are presented in 2-D stress space. In those plots, only two normal stress components are used as axes and therefore they represent the principal stress space (shear components left equal to zero). Additionally, the principal stress axes should coincide with the material axes. It is the general convention that the x-axis corresponds to the rolling direction (0°) of the sheet and the y-axis to the transverse of the rolling direction (90°).

Differences in micro-structure, from rolling, lead to different behaviors in sheet
With this configuration of the axes, it is possible to define different forming states on the yield locus as shown in the figure below. The first thing to note is that any stress state lying within the ellipse does not cause any plastic flow. Stress states should be on the yield locus for the plastic flow. Stress states outside of the yield locus are inadmissible. So, the material is either in elastic region (stresses within the yield locus) or in plastic region (stresses on the yield locus). There are no other options.

Different stress states identified on a yield locus representation
The main advantage of these 2-D representations is that we can plot different forming states on the yield locus. These points are then used to characterize the sheet materials. By plotting two yield loci over another, it is possible to see differences of two materials, for instance, if they behave similar in equibiaxial tension or uniaxial tension or shear.
The yield function is an important part of the puzzle when considering material behavior; it characterizes the 3-dimensional behavior of sheet metal. With it, simulation can predict the changes in yield stress during deformation or strengthening of the material as a result of cold work. This behavior is governed by the hardening model and will be covered in a future blog post.
See the next part of this material series here.












[…] already discussed in Sheet metal plasticity visualized (part one) there are four main components needed to model the plastic deformation of sheet metals: yield […]
[…] posts Materials Matters- “The known unknowns” and “Material plasticity visualized” covered the general aspects, common terminology, and formulation of the plastic properties in […]