A Look Into the Past
While it’s constantly developing and updating, tube hydroforming technology has been around for quite some time — enabling the creation of intricate, cost-saving parts. This is entirely thanks to the hard work of past generations of engineers, who derived complex mathematical representations of tube hydroforming processes. These equations simplified difficult concepts so tooling engineers could understand and implement them in a timely manner. Before building the tools, engineers would plug their data into these equations, achieving a starting point for a process that would yield a feasible part. However, due to advancements in simulation, trial by fire is no longer necessary. So how do these equations from the past hold up to today’s technology? Let’s take a look at one example…
To calculate optimal parameters for a tube forming process, one would likely use some variation of the calibration calculation proven by Altan, shown below in Figure 1.
 Figure 1 – Altan calibration pressure equation
Figure 1 – Altan calibration pressure equation
The resulting pressure is dependent on a few parameters: material yield strength, minimum part radius, and wall thickness. This equation is accompanied by certain assumptions, such as the use of homogeneous tubes. While this may get the ball rolling, things get tricky when parts become increasingly complex. Simulation picks up where textbooks left off. Multiple calibration pressures can be tested in a matter of minutes, allowing for processing decisions to be made in a snap.
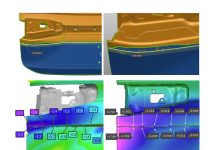
As an example, we can take the simulation of a relatively simple brake pedal part. First, a simulation was run with a calibration pressure of 79.1 MPa, calculated using Altan’s equation. This yields a contact distance of 5 mm between part and tool, which is likely unacceptable by today’s standards (see Figure 2)
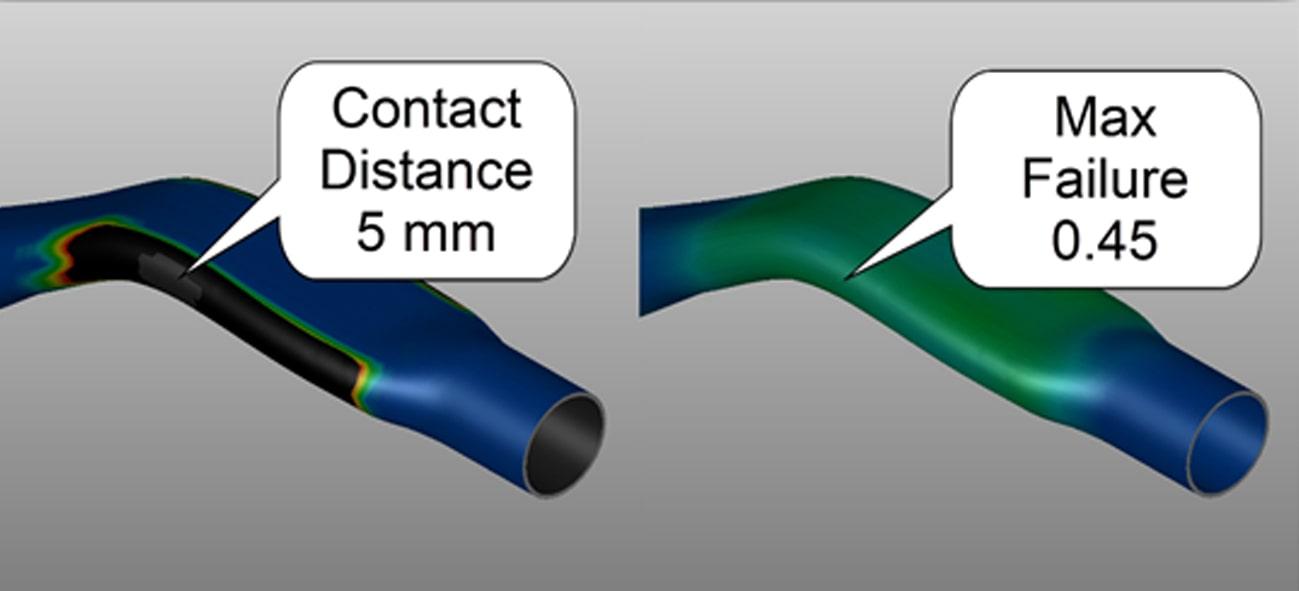
Figure 2 – Contact distance and non-linear max failure based on Altan’s calibration pressure
Rather than guessing at a sufficient calibration pressure, the exact pressure required was determined from a simulation. A systematic optimization simulation allowed for the simultaneous analysis of multiple parameters. In this case, the only process change investigated was the calibration pressure. Using this approach, it was possible to achieve a contact distance within 1 mm between tool and tube
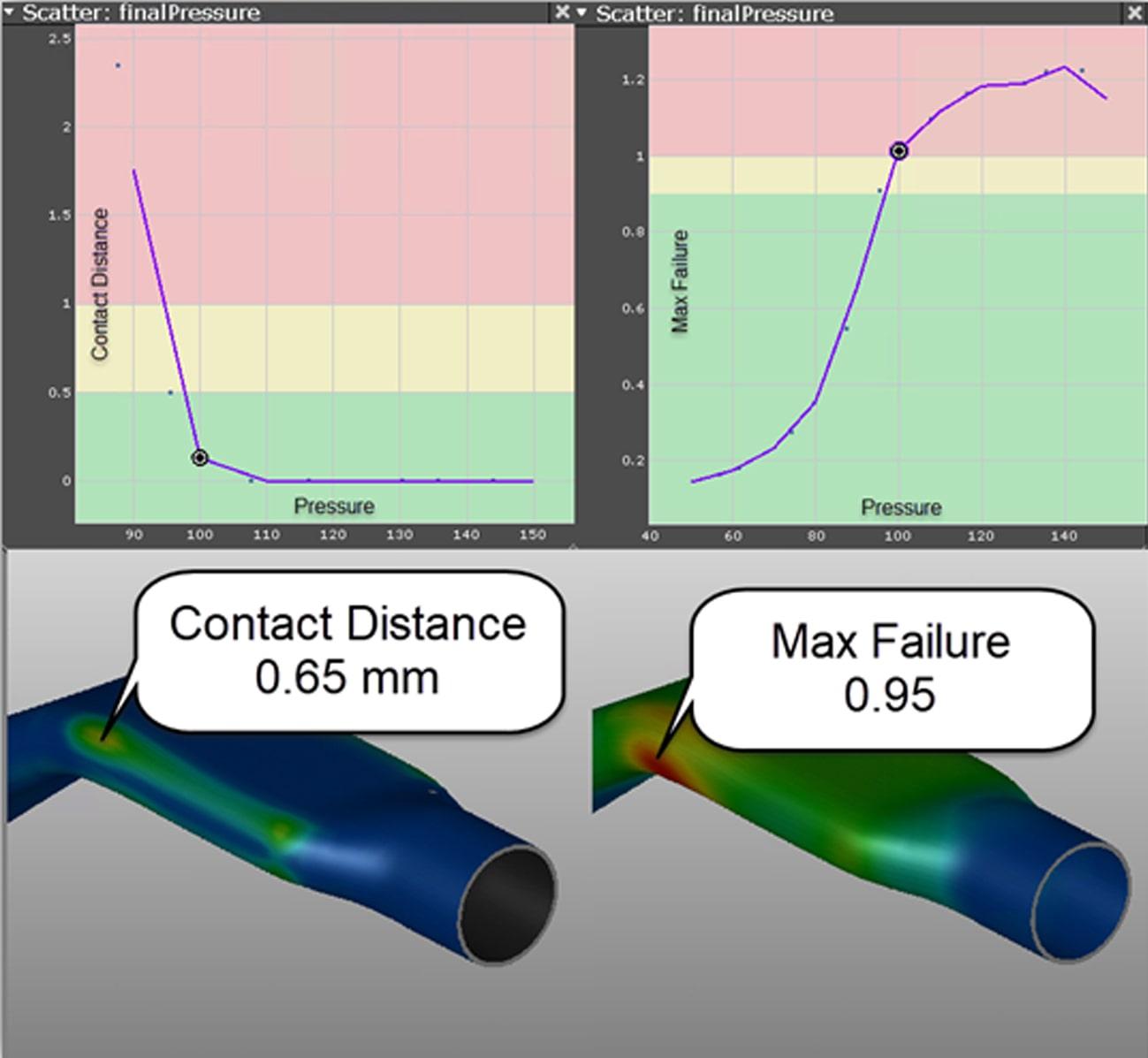
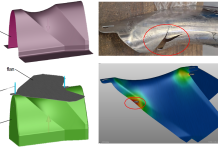
Figure 3 – (Left to Right, Top to Bottom) Contact Distance Vs. Pressure, Max Failure Vs. Pressure, Optimized Contact Distance Result, Optimized Max Failure Result while the material was kept below its failure limit per the FLD (forming limit diagram), shown below in Figure 3.
These results paint a clear picture of the process limits window. There is very little wiggle room with the applied pressure: too high and the part will split; too low and the part will not fall within the 1 mm part deviation specification. It turns out a calibration pressure of 96.5 MPa, rather than the 79.1 MPa calculated with Altan’s equation, provides the best results. Had the contact distance not been within spec when the part splits, the engineer would have to alter the process.
This is not to say that simulation has replaced the experience of past engineers. Rather, simulation makes engineers more effective by allowing them to implement trial runs, with the only cost being man hours and simulation time — without the tooling cuts and other miscellaneous costs related to the trial and error method on the floor. The equations presented still hold true for simpler parts and processes, especially as a first approximation. However, these equations struggle with the automotive industry demanding quicker turnaround and increasingly complex parts, all at a lower price. Using the simulation approach will not only yield a better part, but also a lower cost (see Figure 4 below).
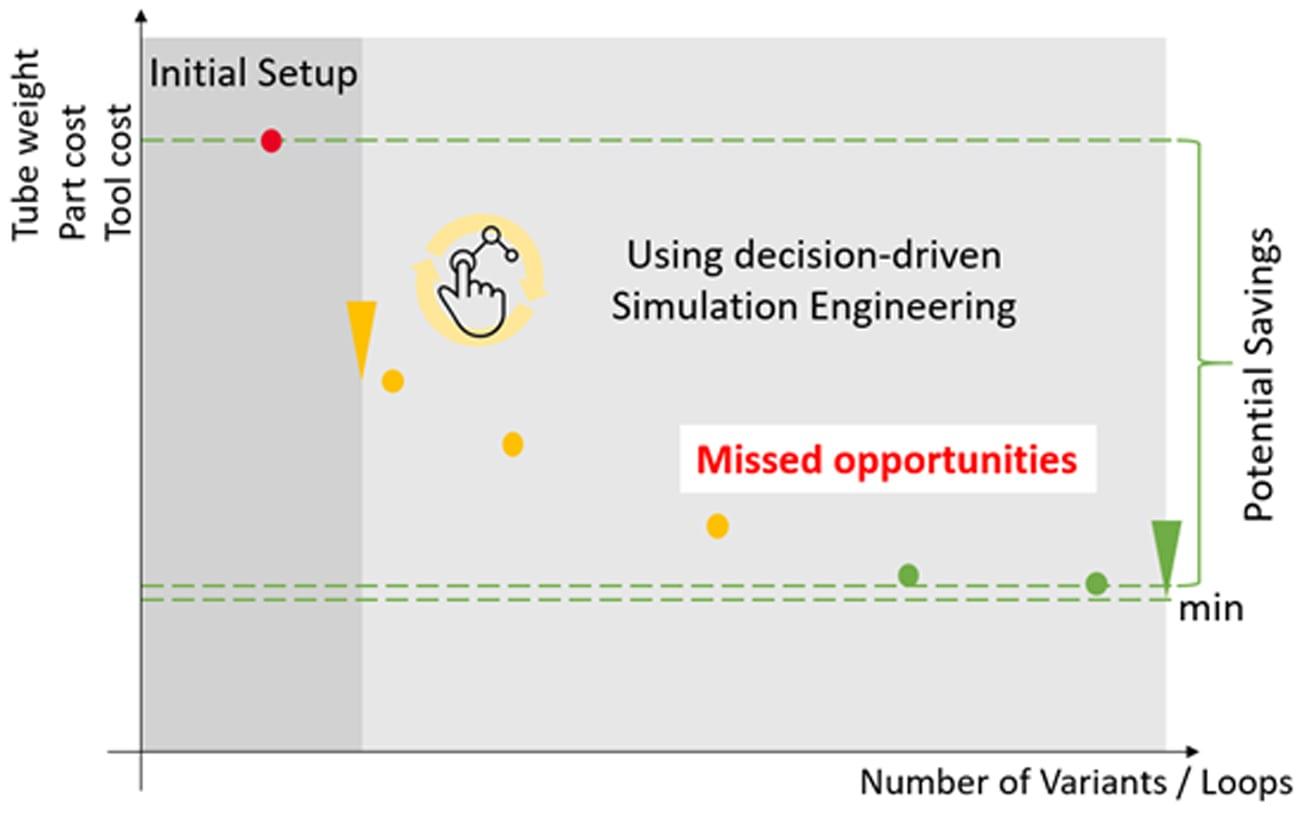
Figure 4 – Potential savings from running simulations before tool build
The ability to quickly calculate a series of process changes and tool changes prevents the painstaking practice of re-cutting tools or re-designing a process after discovering it was inadequately engineered.