Withstanding Variations in Sheet Metal Properties
to Achieve Robust Stamping Processes
When you design a component (of an automobile, household machines, or anything) you want to be sure that this part would be safe under worst conditions (car crash, bad weather, higher loading forces, etc.). In the same manner, a designed sheet metal forming process should also function under worst conditions.
A very common parameter in that respect is the sheet metal itself. You want to make sure that the designed stamping process provides acceptable products with each and every coil used in the whole production life-cycle.
Conventional finite element simulations are deterministic meaning that each simulation is based upon a computer code computing the simulation result of a singular state based on a single set of input parameters. However, the real world is variable, i.e. during a mass production run each individual stamping is produced with slightly changing conditions. Hence one single simulation cannot offer a real image of all the variations that take place in the real world. Yet this is exactly what many simulation companies are still doing, which is the ‘way of yesterday.’
For example, mechanical properties of sheet metals display many variations in reality – from supplier to supplier, from batch to batch, from coil to coil and from continent to continent. Considering how the sheet metals are produced, through melting in a furnace, alloying, heat treatments, rolling operations etc. each process step introduces further variations. Hence, a variation in material parameters like tensile strength, yield stress or r-values are to be expected. Designing a stamping process, of course, we want to guarantee that our process is safe considering these variations.
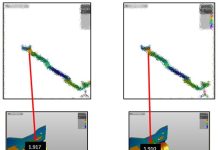
The figure below shows a poorly designed stamping process. The simulation which uses the nominal values of material properties shows a safe process. However, some combinations of the allowed variations are not safe and in those cases the process would fail. Such a process would work perfectly with one coil but could fail with another coil which may be from another batch from the same supplier or may come from another supplier.
The aim should be to design a robust stamping process which can withstand variations in sheet metal properties. In that case the safe process window would cover the whole variation space of the parameters as shown below:
The good news:
The allowable variation of mechanical properties is well-defined and standardized.
This information is also supplied by the material manufacturers and their grades of metal must comply with these set norms in the industry. This allows for first level accuracy in a world of simulation. For example, if you search for a type of steel such as DP600 (HCT600X) you may find such values:
Yield Strength: 340-450 MPa
Tensile Strength: 600-650 MPa
The variation of hardening exponent, n, and the variation of r-values (which define the anisotropy) are in most cases unknown. Mostly a minimum value is given which is used during simulation. These are also derived from the industry standards.
The bad news:
There is no single definition of a worst case material.
If you consider the design of a product, the performance of the final product needs to be measured under service loads or crash test which is the main focus. Therefore, there is a very clear definition of a worst case material; less strength and/or less stiffness. Sheet metal forming is not a single state. It is a process, which makes it difficult to define single worst case material values. Where it becomes even more difficult is that users receive the material information and expect that the values of the Y and T strengths will appear on a table, with ranges of minimum and maximum strengths. Now the user is expected to generate a worst case material value on their own, which is not easy.
If you just consider axisymmetric cup drawing, it is possible to define such guidelines: low hardening exponent and low r-values would lead to less drawing depths. However, the technologically relevant product geometries and corresponding processes are much more complicated and it is very hard to guess the worst combination of parameters beforehand.
So, what is the solution?
Evaluate the feasibility of the process by considering the influence of variation of material parameters, which is exactly what AutoForm has achieved in its simulation solutions. By this way, you can guarantee a robust process since a process window is considered, not a single state. Ideally, this should work as follows:
- Definition of material parameter variations:
- Which parameters should be varied? How large are the variations?
- Statistical combination of material parameters
- In which intervals should I vary the parameters?
- How many simulations are needed to be on the safe side?
- Start simulations and gather results in one single file automatically
- How can I use my computing capacity effectively without manual intervention?
- How can I gather information directly from finished jobs and collect them in one single file for easy handling and archiving?
- Use AutoForm tools for evaluating the simulations
- How can I evaluate results from different simulations at the same time?
- How can I present the robustness of the process with numerical values or color codes using the results from different simulations?
