A New Digital Simulation Methodology to Add Value to the Digital Process Chain and to Support Decision Makers, Reducing Risk and Uncertainty
In this blog post, we introduce a new methodology to ensure digital simulation accuracy to support decision making in the engineering process of sheet metal stampings and to provide the maximum value of digital engineering technology for tool tryout and stamping production.
Although digital simulation has helped to significantly accelerate the stamping engineering process, many loops are still performed in tool tryout, relying on human skill and experience without the support of digital tools custom-tailored for this purpose or meaningful digital documentation to provide full process transparency and traceability. This represents a major hurdle to the full digitalization of the stamping process chain and prevents digital simulations from generating their full potential for cost savings in actual stamping production. Two possible reasons for this may be uncertain prediction capabilities of simulation tools or disconnects in the engineering information flow. In order to maximize the value of digital engineering for production, digital simulation requires a level of reliability or prediction capability to enable proper decision-making processes based only on digital simulation results before going to production.
The exclusive use of deterministic (i.e. single parameter set) simulation results affords only a limited improvement potential and is unable to significantly reduce risks arising from unavoidable production uncertainties [ISO 9001 Risk-Based Thinking]. Deterministic stamping simulations – even when they take into account the full complexity of the stamping process [AutoForm Accuracy Footprint] – are likely to be non-reproducible in reality due to the variation of a large number of input properties! This, of course, is a direct consequence of the well-known fact that the quality performance of the stamped part constantly fluctuates during actual production – depending on where the current stamping process is located inside the process space, defined by all possible parameter variations.
The REM approach described here in greater detail takes such parameter variations into account while assuring full model accuracy using the AutoForm Accuracy Footprint concept. Robustness simulation is a key element of the REM approach of including natural parameter variances into the simulation model (“digital twin”). This allows the generation of a quantitative accuracy index including consideration of accuracy bias and precision, which are also quantitative quality performance indices routinely used in quality management. So what does robustness simulation mean exactly for the quantitative determination of accuracy and the quality index, and how does it support better decision-making leading up to production?
After fulfilling the model accuracy requirements for final validation simulations using the AutoForm Accuracy Footprint, we use robustness simulation to generate a cluster of data points based on distribution functions. Also, the quality targets for the process, i.e. accuracy specification limits (LSL : Lower Specification Limit and USL : Upper Specification Limit) which are normally identical to quality specification limits (LCL : Lower Control Limit and UCL : Upper Control Limit) – as illustrated in Fig 1. – also need to be defined.
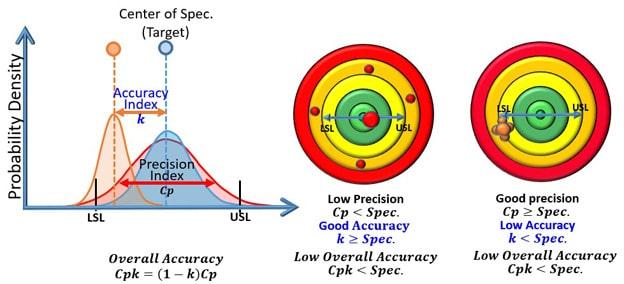
Fig 1. Quantitative Accuracy Indices (equal to Quality Indices)
The accuracy Index is an absolute value indicating the normalized distance from the specification center to the data point average, varying from zero to 1.
The precision index (or process capability) is a measure of the potential result bandwidth. If the actual result bandwidth is less than or equal to the specification range bandwidth, we have perfect precision or process capability since the scatter of all possible outcomes is smaller than the bandwidth of the target range. However, this does not mean that all outcomes lie within the target range. That measure is indicated by the overall accuracy index.
The overall accuracy (or process capability index) indicates that indeed all possible outcomes lie within the target range, indicating perfect result accuracy.
Unlike those of a deterministic simulation, robustness simulation results evaluate all plausible process outcomes, which – of course – forms the basis for supporting and improving the engineering decision-making process.
In the left graphic in Fig. 1, the red-colored shots are high in accuracy but very low in precision. In the right-hand graphic, the orange-colored shots are high in precision but poor in accuracy, i.e. they are far away from the target range. Selectively checking each simulation, we can determine how to improve the precision of the red shots and the accuracy of the orange shots. Of course, we can quantify the problem to improve engineering with the quantitative accuracy index. For the red shots, if gives a value for the failures of about 10,400 per million. Of course, this would not be acceptable for a production process associated with very high predictive & preventive maintenance costs. In other words, consistent precision is strongly requested by production engineering, but if accuracy is not satisfied, the result is huge maintenance and quality control costs during production.
In the right-hand graphic, for the orange shots, if results in part failures of about 620,000 per million. Of course, this would also be a no-go for a production process since 62% of production would have to be scrapped.
Using robustness analysis and determining the result accuracy using the same techniques as in production engineering, process engineers are fully capable of making go/no go decisions and finding solutions for “no go” scenarios. Moreover, using the REM approach, process engineering can contribute meaningfully to the resolution of cost & quality balancing issues for future production and further improve cost & quality with adaptive process control techniques.
One exemplary case for the improvement of decision-making processes using the Robust Engineered Model Approach can be found right here in the formingworld.com blog: “Finding Those Cracks with a Robustness Analysis”. This blog tells the story of how the Robust Engineered Model Approach supports decision making during the final process validation stage.

Fig 2. Risk-based decision-making using REM
This provides very simple and clear evidence that the REM approach will help us to improve the decision-making capabilities of process engineers. From Fig. 2(a), the total accuracy and process capability index indicates a “no go” situation. And from Fig. 2(b), the accuracy position for quality performance is too close to part failure, which also indicates poor accuracy – insufficient to secure the quality specification lower limit. Using this information, a process engineer can now investigate how to first improve the accuracy level (formula below) by focusing on part and tool geometry. ![]()
Using only deterministic simulation results, process engineers would neither have a clear picture on the nature or location of the problem – nor would they have an idea of what to do to resolve the anticipated issues.
Hence, the REM approach is vital for making timely and proper engineering decisions. Adopting this approach as the engineering standard for toolmakers, part producers and automotive OEM’s would generate significant benefits – preventing production issues and avoiding costs while even further reducing time-to-market for stampings.













