Why is springback worse for HSS and AHSS?

It seems that you cannot have a discussion about High Strength Steel (HSS) and Advanced High Strength Steel (AHSS) without springback shortly becoming the center of attention. Springback in high strength steels is the center of much on-going research. Surprisingly, we still hear many people complain that they don’t understand why springback is “all of the sudden” an issue  when it was not an issue with previous materials.

First to define Springback-

the capacity or tendency of a bent or shaped elastic-plastic material (such as a metal) to revert to its original form < Scientific American>

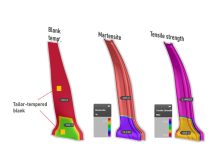
Springback can be illustrated using stress-strain diagrams as obtained during uni-axial tensile tests. In the figure below, a tensile test specimen is shown at three different states during such a test. As the sample is stretched within the testing machine, we measure the amount of stretching and the resulting force in the material. Along the curve highlighted with the letter A, we would see the machine deform the material, making it longer than the original sample. During that portion of the test we would see the material linearly increase its resistance force to the deformation. During this linear load-deformation (stress-strain) relationship all deformation within the material is considered to be “purely elastic”.

Material undergoes pure elastic deformation (A), elastic-plastic deformation (B), and springback (C)

At one point during the test, the material will exhibit a diminishing increase in reaction force. This tendency to increase resistance in the material by a now diminishing amount, is an effective yielding of the material to plastic or permanent deformation. When we isolate the point where purely elastic behavior stops and shows signs of yielding, we call that point the Yield Point of the material. The measured stress in the material (load/area) at that point is known as the Yield Stress, or Yield Strength of the material.

After deforming the part we could reduce the load and allow the part to relax. We would note a decrease in the load within the material that is again linear to the amount of stretching, or strain, applied to the material; C. This linear relationship will be proportional to the relationship noted during the initial deforming of the material along curve A, computing the slope in those areas would indicate a parallel slope. Once the load is completely removed material we would observe that the sample is now permanently longer than original. The difference between the original length and the final length can be measured and reported as a percentage that we call the Plastic Strain; it represents the permanent change in shape of the sample. The difference between the length of the part while under peak load and its final shape is what we can call elastic strain, or springback.

Springback is proportional to the forming stress divided by the elastic modulus

If we isolate the slope of regions A and C, we observe that we can describe a right angled triangle that has the slope of the triangles height divided by the base. The base of the triangle is the measure of elastic strain in the part. The height of the triangle is the limit of load applied during the portions of the test A and C. In the case of A the height of that triangle is the materials observed Yield Strength, for C the height of the triangle is the peak forming stress in that sample. Therefore a simple relationship can be derived to associate the springback in a material to its forming stress, which in the case of planned manufacturing deformation should be greater than the yield strength.

Predicting springback is a matter taking the forming stress in your deformed material and dividing it by its elastic modulus. If the math is that simple, then why is there all the fuss about springback prediction being difficult for these higher strength materials?

As the initial material strength increases, so will forming stress and springback

Consider the illustration above where we look at this simple example but with the assumption that we now have another piece of material that arrives with a higher initial yield strength.If t were possible to during the manufacture of this part achieve the same strain during the forming operation (the new material is formed in the same tool as the first example) then the total strain in the part while the tool is fully engaged remains the same in each case. As the tool disengages from the material then we again see the elastic behavior described by the materials elastic modulus. However, since the forming stress in the second material is higher than the first samples, we will see a proportional increase in the elastic strain and therefore more springback. In essence a smaller proportion of the total strain in the tool is plastic and a greater proportion of the overall strain is elastic. In this very simple example the two materials are illustrated with yield stresses of 200 and 250 MPa—a 25% increase in material strength. Therefore a 25% increase in observed springback behavior is likely.

It follows that if you double the initial yield strength of a material you double that materials potential for elastic strain and therefore should expect greater springback. It is not mystery then that when we move from product designs that previously used 200 MPa materials to materials with Yield Strengths approaching 600 MPa that the effective tripling of springback potential has made producing those parts far more difficult.

Alternative materials like Aluminium, which has a lower Elastic Modulus, also will display different springback behavior. Aluminiums elastic modulus is ~70GPa or 70,000MPa–approximately one third that of steel. Therefore, it is expected that Aluminum will have 3 times the springback effect.

It seems that it should be simple enough, but still it is not so elementary. In all the examples so far we have assumed that the part might be formed with a fairly uniform strain or stretch, which we could use as a baseline to compute the in-die forming stress and therefore predict the springback. But unfortunately this is not the case. It is more likely that within a given part the strain distribution throughout the part is not uniform.

Different areas on the same part undergo different deformation and have different springback

In reality we are not producing simple test samples being stretched uniform amounts. Real parts will have strain different strains distributed throughout the part. And strain distributions that vary from part to part during normal production conditions. When any aspect of the forming process changes we too could see differences in the distribution of in tool stretching, which changes the distribution of springback effects through the part and possibly very different effect on final part shape.

• How do you plan for and accommodate the possibility of varying springback in your parts during production?
• What measures do you take to correct for springback to assure the correct products for your customers?

Springback will be another ongoing topic of discussion here, we look forward to your input as we “think in Sheet Metal.”