Impact of Flow Conditions in Cooling Channels on Thermal Cycling Part Three

By
Michael Düring, AutoForm Product Manager
-
0

Part Three: Needed or Not? Computing Flow Conditions Inside Cooling Channels.

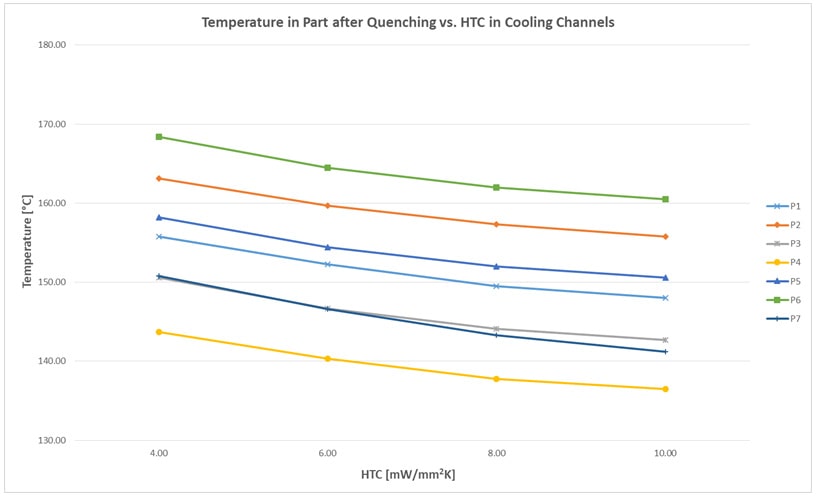
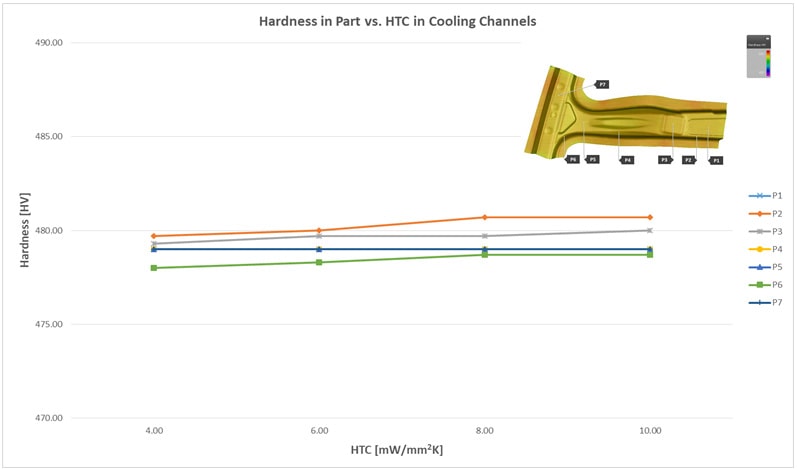
The impact of the position of the cooling channels embedded in the tool on final part quality has been the focus in past blog posts. In our previous post, addressing the necessities of modelling of local flow rates, pressure distributions, and thus finally the Heat Transfer Coefficient, Michael Düring, Product Manager at AutoForm mentions: ‘We found that in computing the flow conditions the impact was so negligible, and its effect was so slight in the end, that compared to working without it you would come to the same conclusion; that this is something which can safely be disregarded.’ Here in part three of this series we publish the actual study that supports that bold claim. This post is based on a paper titled ‘Impact of Flow Conditions in Cooling Channels on Thermal Cycling’ 2017, by Kannan Kidambi, Thomas Brenne and Michael Düring. The actual paper is available for download at the end of this post. The authors were able to show that even though an intentionally bad distribution of cooling channels in the tool bodies can lead to a pronounced inhomogeneity of the temperature field on the tool surface under regular process conditions (commonly called ‘hotspots’), such kind of inhomogeneity has a very limited influence on the quality of the final part. This is valid in particular for the resulting hardness. It seems that the order of heat conduction in the tool and the sheet itself, combined with damping effects of the heat transfer at the contact interfaces dominate the thermal system. While the authors of the study express their opinion that there is almost no influence of the flow conditions in the cooling channels on final part quality, others consider flow condition control as a vital prerequisite to achieving high quality parts. The latter consider that extensive CFD-studies towards accurate prediction of tool surface temperature distribution is crucial to do a dead-on prediction of final part quality outcomes from forming simulation. This is naturally linked to remarkable additional efforts spent in terms of installing equipment, modeling and computation. Variation of temperature distribution in a quenched part Exemplarily, a real tool geometry for a B-pillar has been converted into a model in AutoForm. The process itself was computed using AutoForm-ThermoSolverplus. All measures are taken from the same model configuration and controls settings. Subsequently, the HTC representing the interface between cooling media and cooling channel boundary has been varied representing modified flow conditions. Values between 4 and 10 mW/mm2K have been assumed. These values lead to remarkable differences in terms of tool surface temperatures. The impact on the temperatures in the sheet after quenching is far more moderate: at the end of the quenching stage, the range of predicted temperatures at any of the observed points on the sheet, over the applied HTC range of 4 to 10 mW/mm2K, are observed to be within a range of around 5% – as shown in Figure 1. This indicates that the evolution of the cyclic (steady state) temperature fields is also not affected in a way that could lead to remarkably higher or lower cooling rates in the sheet material. Based on the given tool design this can be easily proven. Since we are assessing this effect entirely virtually, these effects can be investigated further with ease.
  Figure 1. Temperature evolution in part Evolution of hardness in part As mentioned, the described effects translate only in slightly affected cooling rates at the selected points. It becomes clear, that the generated hardness values cannot be strongly controlled by modifying the heat transfer coefficient between the cooling medium and cooling channel boundaries. Since the HTC is the result of the current conditions which have been assumed to be integrally changing, this leads to the observation that there is almost no practical way to significantly affect the part quality outcome just by flow rate control. This may also help answer the question of how local inconsistencies of flow conditions in certain areas of the tool design can influence the distribution of temperatures in the contact areas. It seems to be more than unlikely that major effects in terms of part’s hardness can result from HTC variations in a reasonable range. The considered part in combination with the tool set is clearly not sensitive to integral changes of flow conditions (Figure 2). Hardness values are predicted to only be moderately affected. This means that the detailed design of cooling channels can lead only to minor order impacts. In other words, for a given design of channels in a tool, varying flow conditions do not provide a good handle to actively influence part quality outcomes for hot forming processes.
  Figure 2. Hardness in part
  Figure 3. Process ramp-up cyclic behavior There is a moderate difference in peak temperatures at the selected point (point 6) over the cyclic ramp-up to steady state conditions. However, there is a one-cycle difference between the two HTC extremes in how quickly steady state is achieved: 5 cycles for HTC 4 mW/mm2K versus 4 cycles for 10 mW/mm2K. This seems to be a negligible effect that does not need any further attention. The surface area of the cooling channels, defined by length and diameter can be roughly calculated by balancing incoming energy amounts with the extracted heat amounts by means of water cooling to be designed. Literature indicates how the relationship between the diameter of the cooling channels and the enforced flow rate can govern the Reynolds number as a measure for the cooling medium’s flow state. Conclusions Referring to the question to which extent efforts in planning and calculation of cooling channel flow conditions are beneficial, a real tool geometry has been used. The variation of the flow conditions – represented for instance by the cooling media flow rate – gives the opportunity to the engineer to virtually assess common effects by means of FE-code. It has been shown – in the paper – that a variation of the flow rate – still in reasonable limits – can lead to a pronounced variation of peak temperatures at the tool surfaces after quenching – still in reasonable limits – can lead to a pronounced increase of peak temperatures at the tool surfaces after quenching. But, it has also been shown that this does not directly translate into noticeably higher or lower peak temperatures in the part – which indicated a limited effect on cooling rates and hardness. Overall, the process based on realistic tool geometry – can be considered as a less sensitive one. This subsequently leads to the conclusion that generic formula-based approaches can sufficiently serve for the layout tasks of the cooling channel current conditions. One more or less simplified set of formulas for such purpose – still neglecting the local pressure distribution in the cooling channels has been introduced. Download the original paper HERE. Download the original paper HERE. Alternatively, see Part 1 and Part 2 of this series.

RELATED ARTICLESMORE FROM AUTHOR

LEAVE A REPLY

Please enter your comment!
Please enter your name here