Charting the Course to Achieving Highly Accurate Pocess Simulations

AutoForm’s application of the Pareto principle serves to prepare our industry for the next level of achieving greater simulation accuracy. In this multi-part series, Dr. Bart Carleer (AutoForm’s Technical Director) introduces the AutoForm Pareto Principle applied to sheet metal forming simulation and explains how understanding this principle helps to efficiently achieve simulation accuracy for the stamping industry.

Series Index: Part 1, Part 2, Part 3, Part 4, Part 5, Part 6

The Pareto Principle in Simulation

The Pareto principle states that 80% of consequences result from 20% of the causes. Management consultant Joseph M. Juran developed this principle in the context of quality control and quality improvement. Named after the Italian economist Vilfredo Pareto, this 80/20 rule is mathematically described by a power law distribution, also known as the Pareto distribution. This power law distribution is valid for a particular set of parameters, so you can already imagine how this might apply to setting up part forming simulations. Yet many natural phenomena are shown to adhere to this law.

In computer science, for example, the Pareto principle can be applied to optimization efforts. In its early days, Microsoft noted that the top 20% of the most reported bugs were responsible for causing 80% of related errors and crashes in a given system. By fixing this top 20% of all bugs, 80% of the errors were eliminated. Microsoft learned to fix the important issues first.

This principle, as presented in our AutoForm Pareto principle chart, can also be applied to achieve and improve simulation accuracy. To start, we need to determine the essential input parameters needed to achieve accurate simulation results (i.e., those that most significantly influence the simulation results). With this knowledge, we can focus on those aspects first to make sure we have the essential parameters defined and validated. These then form the basis for a simulation representing 80% of the future reality of the die shop floor.

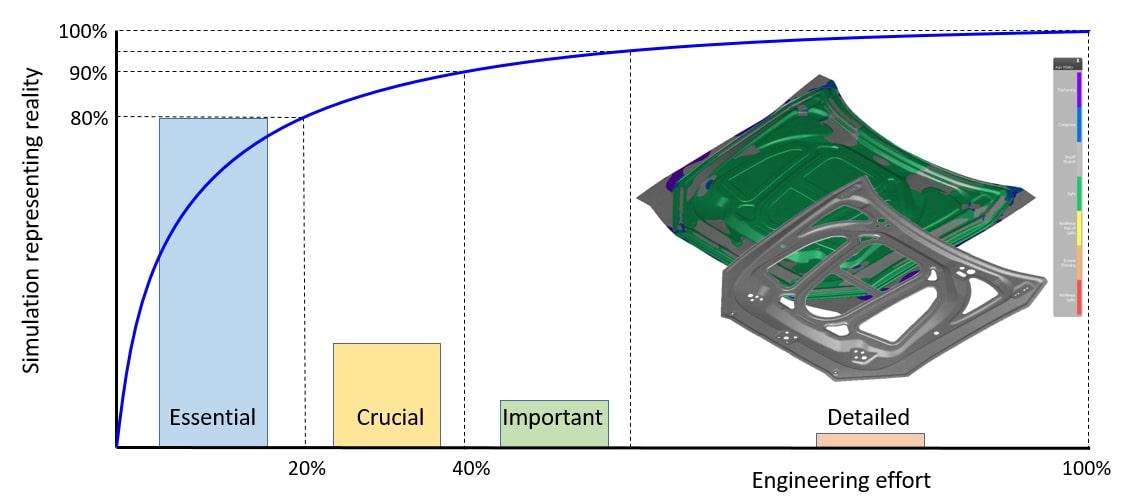
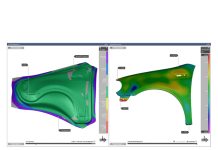
Figure 1: Simulation input parameters and their impact on simulation results

Once all the essential parameters are under control, we then have a solid base for accurate simulation results and can move on to the next class of parameters – bearing the Pareto principle in mind.

The next group of input parameters, which we define as the crucial parameters, also contribute to overall accuracy – but not quite as significantly as the first group of essential parameters. By reapplying our understanding of priorities, we can build up subsequent parameters to evolve our simulation towards increasing accuracy. Yet in consideration of priorities, we also determine which parameters contribute very little to ultimate accuracy. After all, it doesn’t make sense to dedicate a great amount of time to fine-tuning the least impacting aspects if the parameters with more significant influence on the simulation result are not secured and validated yet. Neither does it make sense to skip over major impacting aspects, ignoring them for later, as this violates the concept of a growing accuracy footprint.

So, the AutoForm Pareto Principle does not only provide guidance on the impact of different parameters on the simulation result, but it also suggests an engineering-based model building process, working from the more significant to the less significant input parameters. In this way, it helps us to systematically build a consistent and accurate simulation model.

Applying the AutoForm Pareto Principle to Process and Simulation Maturity

During the early phase of feasibility studies and process design, there are both “knowns and unknowns.” During the development chain, part parameters become increasingly concrete and defined so that the Pareto principle considers them in terms of increasing process maturity while simultaneously increasing simulation maturity.

Our visual representation of the Pareto principle provides four groups of data-entry for engineering parameters. Importantly, the essential parameters, crucial parameters, important parameters and the detailed parameters should be input in the right sequence! The basis of the Pareto principle is that only 20% of the parameters (classified as the essential parameters) contribute around 80% to the overall simulation accuracy. Furthermore, we observe within the Pareto principle that the successive parameters still contribute to overall accuracy, yet they provide a declining contribution to the total accuracy.

What this also means is that generally it doesn’t make sense to spend a lot of time on less significant parameters as long as the more significant parameters are not yet validated.

Considering this as the stamping process development chain, we can clearly identify several (general) milestones, which concern our investigation into the nature of accuracy:

At the very early phase, the target achievement is theme selection. Only the basic styling and first CAD geometries are available. The focus is mainly on the geometry and the function of the part. No detailed process definition exists, so engineering only focuses on part feasibility.

One of the early milestones is part design freeze. Now, engineering goes beyond feasibility and focuses more on part manufacturability and process feasibility. Details are added, such as material specifications, and a press is selected or the press shop is known. The number of operations required to produce this part is decided and several processing units are assigned to those operations.

Die design and 3D construction are both happening at the same time. In completing the 3D die design data, we determine how the die should appear. The simulation input considers which forces are acting through the die.

The next important milestone is release for milling. At this point in time, all manufacturing data should be known: the complete forming process and stamping process has been defined and validated and this data is released. Here, we are leaving the virtual world and enter the physical world to begin producing the tools.

Last but not least, the proof in the pudding becomes apparent during the die tryout phase. We commence part stamping and see the rewards of engineering concepts created months earlier. We can observe the entire system working because the physical process is working according to what has been engineered.

Observed through the lens of the Pareto principle, you can see that during this development chain, more and more aspects became concrete and defined, and are subsequently reflected in the process definition. The maturing of the process definition goes hand-in-hand with the maturing of the simulation model. The more simulation-supported decisions are made, the more the process matures and the simulation increasingly represents the future reality and becomes geared towards true accuracy. The ultimate level of accuracy is achieved when the real result matches the simulation result.

The implication for the process chain is that the physical process should be a true representation of the engineered virtual process. So we dedicate all of our engineering efforts to achieving a very smooth tool tryout and, later on, a very smooth production of this part.

The visual representation of the Pareto principle teaches us that we should strive for an accurate result based on the available information we have. As little information is present at the early phase, we still have to make sure we can achieve the “best possible” at that point. Yet every phase of digital development is the best possible, given the circumstances. Through this series, I shall explain this point in detail.

Along the process chain, we should take into account the availability of data at a certain moment in time. What do we know, what is already defined, and which decisions are still open? What assumptions do we have to make at this point? The Pareto principle also teaches us that we should consider which aspects contribute to which level of maturing accuracy. It doesn’t make sense at the early phase to focus on small details, which in the end contribute very little to overall accuracy. The Pareto principle diagram shows that such details only contribute 5% to overall accuracy. And, the focus on details often confuses the bigger picture, leading to a loss of focus, time, money and effort.

At the same time, in creating assumptions and modeling certain aspects, we have to ensure that all of the definitions applied in our simulation can be transferred to reality. Our goal is not to create an abstract numerical value, but later on, to create the physical model twin – in the physical world, in the die shop.

The key takeaways of this first part of our blog series are that to strive for (maximum) accuracy along the stamping process chain, we should take into account:

• The availability of process data at each specific moment in time
• Which input values contribute by which percentage to the ultimate result accuracy
• The logical sequence of input value definitions – from the essentials (first) to the details (last)
• How definitions in the simulation model can be transferred into reality

Over the next parts of this series, we will explore application of the AutoForm Pareto Principle in greater detail. See part two here!